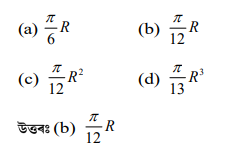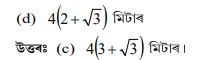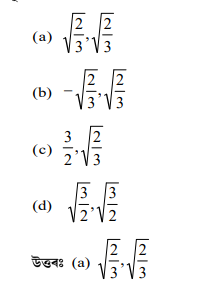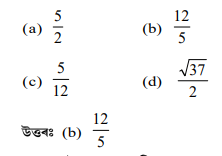আপুনি যদি অসমীয়া মাধ্যম Class 10 ৰ ছাত্র বা ছাত্রী হয় তেনেহলে নিচ্ছই আপুনি ইন্টাৰনেট ত Class 10 Maths MCQ Chapter 9 ত্রিকোণমিতিৰ কিছুমান প্রয়োগ Assamese Medium সমাধান বিচাৰি আছে? হয়। চিন্তা নকৰিব, আমাৰ এই প্রবন্ধত অসমীয়া মাধ্যমৰ Class 10 Maths MCQ Chapter 9 ৰ সম্পূৰ্ণ সমাধান বিনামূলীয়া কৈ যোগান ধৰা হৈছে।
Class 10 Maths MCQ Chapter 9 ত্রিকোণমিতিৰ কিছুমান প্রয়োগ
অধ্যায় – ৯
ত্রিকোণমিতিৰ কিছুমান প্রয়োগ
বহু বিকল্পধর্মী প্রশ্ন-উত্তৰ (MCQ)
প্রশ্নঃ যদি সূৰ্যৰ উঠন কোণ 45° তেনেহ’লে এটা স্তম্ভ আৰু ছাঁৰ অনুপাত হ’ব-
(a) 1:1
(b) 1:2
(c) √2:1
(d) 1:3
উত্তৰঃ (a) 1:1
প্রশ্নঃ সমান ব্যাসার্ধৰ এটা বেলন আৰু এটা শংকুৰ বক্রপৃষ্ঠৰ কালি সাংখ্যিকভাবে সমান। যদি বেলনটোৰ উচ্চতা 2 cm, তেনেহ’লে শংকুটোৰ হেলনীয়া উচ্চতা হ’ব- HSLC 25
(a) 2 cm
(b) 4 cm
(c) 6 cm
(d) 8 cm
উত্তৰঃ (b) 4 cm
প্রশ্নঃ এটা ট্রেপিজিয়ামৰ কালি 1350 m² আক ইয়াৰ সমান্তৰাল বাহুবোৰৰ দীঘৰ সমষ্টি উচ্চতাৰ তিনিগুণ হ’লে, উচ্চতা হ’ব HSLC ’24
(a) 20 m
(b) 10 m
(c) 60 m
(d) 30 m
সমাধানঃ (d) 30 m
প্রশ্নঃ ভূমিত এটা স্তম্ভ উলম্বভাবে থিয় হৈ আছে। স্তম্ভটোৰ পাদবিন্দুৰ পৰা 15 মিটাৰ দূৰত্বত ভূমিত থকা এটা বিন্দুৰ পৰা স্তম্ভটোৰ শীর্ষবিন্দুৰ উঠন কোণ 60° পোৱা গ’ল। স্তম্ভটোৰ উচ্চতা হ’ব-
(a) 30 মিটাৰ
(b) 15 মিটাৰ
(c) 15√(3) মিটাৰ
(d) 30√(3) মিটাৰ
উত্তৰঃ (c) 15√(3) মিটাৰ।
প্রশ্নঃ 1.5 মিটাৰ ওখ পর্যবেক্ষক এজনে এটা চিমনীৰ পৰা 28.5 মিটাৰ আঁতৰত আছে। তাইৰ চকুত চিমনীটোৰ উঠন কোণ 45°। চিমনীটোৰ উচ্চতা হ’ব-
(a) 20 মিটাৰ
(b) 30 মিটাৰ
(c) 40 মিটাৰ
(d) 57 মিটাৰ
উত্তৰঃ (b) 30 মিটাৰ।
প্রশ্নঃ সূৰ্যৰ উন্নতি 60° হ’লে 30 মি. দৈর্ঘ্যৰ ছাঁ উৎপন্ন কৰা উলম্ব স্তম্ভ এটাৰ উচ্চতা হ’ব-
প্রশ্নঃ R ব্যাসার্ধৰ এটা বৃত্তৰ কেন্দ্ৰত 30° কোণযুক্ত বৃত্তকলাৰ কালি হ’ব- HSLC 25
প্রশ্নঃ এটা বহুমহলীয়া অট্টালিকাৰ শীৰ্ষৰ পৰা এটা মিটাৰ ওখ অট্টালিকাৰ শীৰ্ষ আৰু পাদবিন্দুৰ পতন কোণ যথাক্রমে 30° আৰু 45°। অট্টালিকা দুটাৰ মাজৰ দূৰত্ব হ’ব-
প্রশ্নঃ 75 মিটাৰ ওখ স্তম্ভ এটাৰ ওপৰৰ পৰা বস্তু এটাৰ পতন কোণ 30° । তেতিয়া স্তম্ভটোৰ পাদবিন্দুৰ পৰা বস্তুটোৰ দূৰত্ব হ’ব-
(a) 25√(3) মিটাৰ
(b) 50√(3) মিটাৰ
(c) 75√(3) মিটাৰ
(d) 150 মিটাৰ
উত্তৰঃ (a) 25√(3) মিটাৰ।
প্রশ্নঃ 3x² – 2√6 x + 2 = 0 সমীকৰণটোৰ মূলবোৰ-
প্রশ্নঃ এটা স্তম্ভৰ পাদবিন্দুৰ পৰা 30 মিটাৰ আঁতৰত ভূমিত থকা এটা বিন্দুৰ পৰা স্তম্ভৰ শীৰ্ষৰ উঠন কোণ 45° হ’লে স্তম্ভটোৰ উচ্চতা-
(a) 30 মিটাৰ
(b) 15 মিটাৰ
(c) 10 মিটাৰ
(d) 60 মিটাৰ
উত্তৰঃ (a) 30 মিটাৰ।
প্রশ্নঃ এটা দ্বিঘাত বহুপদ ৰাশিৰ দুটা ভিন্ন শূণ্য থাকিলে লেখডাল x-অক্ষক ছেদ কৰা বিন্দুৰ সংখ্যা হ’ব- HSLC’24
(a) 2
(b) 3
(c) 1
(d) 4
সমাধানঃ (a)2
প্রশ্নঃ এখন নদীৰ ওপৰেদি থকা দলং এখনৰ এটা বিন্দুৰ পৰা নদীখনৰ দুই বিপৰীত ফালৰ পাৰৰ পতন কোণ যথাক্রমে 30° আৰু 45°। যদি দুই পাৰৰ পৰা 3 মিটাৰ উচ্চতাত দলংখন থাকে তেনেহ’লে নদীখনৰ প্ৰন্থ হ’ব-
(a) 4(3 + √(3)) মিটাৰ
(b) 3(1 + √(3)) মিটাৰ
(c) 2(3 + √(3)) মিটাৰ
(d) 3(3 + √(3)) মিটাৰ
উত্তৰঃ (b) 3(1 + √(3)) মিটাৰ।
প্রশ্নঃ এটা উলম্ব খুটাৰ ছাঁৰ দৈর্ঘ্য ইয়াৰ উচ্চতাৰ √3 গুণ হ’লে সূৰ্যৰ উন্নতিৰ উঠনকোণ হ’ব-
(a) 45°
(b) 60°
(c) 90°
(d) 30°
উত্তৰঃ (d) 30°
প্রশ্নঃ দুটা বৃত্তই পৰস্পৰে C বিন্দুত বহিঃভাবে স্পৰ্শ কৰে আৰু AB বৃত্ত দুটাৰ উমৈহতীয়া স্পর্শক হলে ∠ACB ৰ মান হ’ব-
(a) 90°
(b) 45°
(c) 60°
(d) 30°
উত্তৰঃ (a) 90°
প্রশ্নঃএটা বিন্দু Q ৰ পৰা এটা বৃত্তৰ স্পর্শকডালৰ দৈর্ঘ্য 24 cm আৰু কেন্দ্ৰৰ পৰা Q ৰ দূৰত্ব হ’লে 25 cm, বৃত্তটোৰ ব্যাসার্ধ হ’ব- HSLC’25
(a) 24.5 cm
(b) 15 cm
(c) 12 cm
(d) 7 cm
উত্তৰঃ (d) 7 cm
প্রশ্নঃ ভূমিত এটা স্তম্ভ উলম্বভাবে থিয় হৈ আছে। স্তম্ভটোৰ পাদবিন্দুৰ পৰা 15 মিটাৰ দূৰত্বত ভূমিত থকা এটা বিন্দুৰ পৰা স্তম্ভটোৰ শীৰ্ষৰ উঠন কোণ 30° পোৱা গ’ল। স্তম্ভটোৰ উচ্চতা হ’ল-
(a) 5√(3) মিটাৰ
(b) 15√(3) মিটাৰ
11 (c) 3 মিটাৰ
প্রশ্নঃ ABC ত্রিভুজত∠A = 90° , AB = 3cm BC = 5cm আৰু AD⊥BC হ’লে AD ৰ দৈর্ঘ্য হ’ব-
প্রশ্নঃ এটা স্তম্ভৰ পাদবিন্দুৰ পৰা 15 মিটাৰ আঁতৰত ভূমিত থকা এটা বিন্দুৰ পৰা স্তম্ভটোৰ শীৰ্ষৰ উঠন কোণ 60° হ’লে স্তম্ভৰ উচ্চতা হ’ব-
