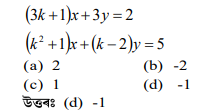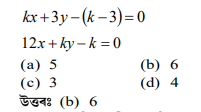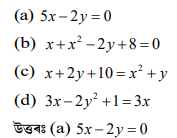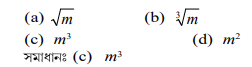আপুনি যদি অসমীয়া মাধ্যম Class 10 ৰ ছাত্র বা ছাত্রী হয় তেনেহলে নিচ্ছই আপুনি ইন্টাৰনেট ত Class 10 Maths MCQ Chapter 3 দুটা চলকত ৰৈখিক সমীকৰণৰ যোৰ Assamese Medium সমাধান বিচাৰি আছে? হয়। চিন্তা নকৰিব, আমাৰ এই প্রবন্ধত অসমীয়া মাধ্যমৰ Class 10 Maths MCQ Chapter 3 ৰ সম্পূৰ্ণ সমাধান বিনামূলীয়া কৈ যোগান ধৰা হৈছে।
Class 10 Maths MCQ Chapter 3 দুটা চলকত ৰৈখিক সমীকৰণৰ যোৰ
অধ্যায় – ৩
দুটা চলকত ৰৈখিক সমীকৰণৰ যোৰ
বহু বিকল্পধর্মী প্রশ্ন-উত্তৰ (MCQ)
প্রশ্নঃ y = mx +3 সমীকৰণৰ y আৰু X ৰ মান সমান আৰু y=3 হ’লে m ৰ মান কিমান?
(a) 2
(b) 3
(c) 0
(d) 1
উত্তৰঃ (c) 0
প্রশ্নঃ তলৰ কোনটো বর্গ সংখ্যা নহয়?
(a) 576
(b) 529
(c) 729
(d) 744
উত্তৰঃ (d) 744
প্রশ্নঃ দুটা চলকত এটা ৰৈখিক সমীকৰণৰ জ্যামিতিক প্রদর্শনটো হ’ল এটা-
(a) অধিবৃত্ত
(b) সৰলৰেখা
(c) বৃত্ত
(d) ওপৰৰ এটাও নহয়
উত্তৰঃ (b) সৰলৰেখা।
প্রশ্নঃ y = 4x ৰ লেখীয় ৰূপ হ’ল এডাল ৰেখা যি ………
(a) মূল বিন্দুৰ মাজেৰে পাৰ হৈ যায়
(b) x অক্ষৰ সমান্তৰাল হয়
(c) x অক্ষৰ লম্ব হয়
(d) y অক্ষৰ লম্ব হয়
প্রশ্নঃ বাপেক আৰু পুতেকৰ বয়সৰ সমষ্টি 65 বছৰ আৰু সিহঁতৰ বয়সৰ পাৰ্থক্যৰ দুগুণ 50 বছৰ। তেতিয়া দেউতাকৰ বয়স কিমান?
(a) 55
(b) 150
(c) 45
(d) 40
উত্তৰঃ (c) 45
প্রশ্নঃ যদি x=2, y = 2 আৰু px+2y-10p = 0 ৰেখা দুটাই এটা বিন্দুত মিলিত হয়, তেন্তে p ৰ মান কিমান? HSLC’25
প্রশ্নঃ একে ব্যাসার্ধ আৰু একে উচ্চতাযুক্ত এটা শংকু আৰু এটা চুঙণ্ডাৰ আয়তনৰ অনুপাত হ’ব- HSLC ’24
প্রশ্নঃ সমাধান নথকা ৰৈখিক সমীকৰণ এযোৰক কোৱা হয়-
(a) অসংগত
(b) পৰতন্ত্র
(c) সংগত
(d) এটাও নহয়
উত্তৰঃ (a) অসংগত।
প্রশ্নঃ দুটা চলকবিশিষ্ট ৰৈখিক সমীকৰণৰ সমাধান কেইটা-
(a) দুটা সমাধান আছে
(b) অসীম সংখ্যক সমাধান আছে
(c) এটা সমাধান আছে
(d) কোনো সমাধান নাই
উত্তৰঃ (b) অসীম সংখ্যক সমাধান আছে।
প্রশ্নঃ p ৰ কি মানৰ বাবে তলত দিয়া সমীকৰণযোৰৰ এটা অদ্বিতীয় সমাধান আছে?
4x+py+8=0,2x+2y+2=0
(a) 2ৰ বাহিৰে সকলো মানৰ বাবে
(b) 3 ৰ বাহিৰে সকলো মানৰ বাবে
(c) 5ৰ বাহিৰে সকলো মানৰ বাবে
(d) 4 ৰ বাহিৰে সকলো মানৰ বাবে
উত্তৰঃ (d) 4 ৰ বাহিৰে সকলো মানৰ বাবে।
প্রশ্নঃ তলৰ কোনটো এটা ঘটনাৰ সম্ভাবিতা হ’ব নোৱাৰে? HSLC ’24
প্রশ্নঃ k ৰ কি মানৰ বাবে তলৰ সমীকৰণযোৰৰ কোনো সমাধান নাথাকে-
প্রশ্নঃ যদি এযোৰ ৰৈখিক সমীকৰণ সংগত হয় তেন্তে ৰেখা কেইডাল
(a) পৰস্পৰ মিলি যায় বা কটাকটি কৰে
(b) পৰস্পৰ সমান্তৰাল হয
(c) সদায় কটাকটি কৰে
(d) ওপৰৰ এটাও নহয়
উত্তৰঃ (a) পৰস্পৰ মিলি যায় বা কটাকটি কৰে।
প্রশ্নঃ x – 2y – 3 = 0 সমীকৰণটোৰ এটা সমাধান হ’ল-
(a) (1,-1)
(b) (0, 1)
(c) (1, 0)
(d) (1, 1)
উত্তৰঃ (a) (1,-1)
প্রশ্নঃ k ৰ কি মানৰ বাবে তলৰ সমীকৰণযোৰৰ কোনো সমাধান নাথাকে-
প্রশ্নঃ তলত দিয়া সমীকৰণ বিলাকৰ কোনটো দুটা চলকযুক্ত ৰৈখিক সমীকৰণ? HSLC’25
প্রশ্নঃ 3x – 5y = 7 আৰু 5y – 6x = 7 সমীকৰণযোৰৰ –
(a) অসীম সংখ্যক সমাধান থাকে
(b) কোনো সমাধান নাথাকে
(c) মাত্র দুটা সমাধান থাকে
(d) মাত্র এটা সমাধান থাকে
উত্তৰঃ (b) কোনো সমাধান নাথাকে।
প্রশ্নঃ কি চর্তত px³ + qx² + rx + s = 0 এটা দ্বিঘাত সমীকৰণ হ’ব- HSLC ’24
প্রশ্নঃ তলৰ ৰৈখিক সমীকৰণৰ যোৰকেইটা বিবেচনা কৰা।
(i) (i) 2x – 3y = 8, 4x – 6y = 9
(ii) (ii) 2x + 3y – 9= 7, 4x+ 6y -18= 8
(a) (i) যোৰটোৰ সমাধান নাই, কিন্তু (ii) যোৰটোৰ অসীম সংখ্যক সমাধান আছে।
(b) (i) যোৰটোৰ অসীম সংখ্যক সমাধান আছে, কিন্তু (ii) যোৰটোৰ সমাধান নাই।
(c) (i) আৰু (ii) দুয়োটা যোৰৰে সমাধান আছে।
(d) (i) যোৰটোৰ সমাধান নাই, কিন্তু (ii) যোৰটোৰ অদ্বিতীয় সমাধান আছে।
উত্তৰঃ (a) (i) যোৰটোৰ সমাধান নাই, কিন্তু (ii) যোৰটোৰ অসীম সংখ্যক সমাধান আছে।
প্রশ্নঃ p(x)= x³ + 4x² – 3x +2: বহুপদটোক x + 1 ৰে হৰণ কৰিলে, ভাগশেষ কিমান হ’ব? HSLC’25
(a) 4
(b) -4
(c) 8
(d) -8
উত্তৰঃ (c) ৪
প্রশ্নঃ তলৰ ৰৈখিক সমীকৰণৰ যোৰকেইটা বিবেচনা কৰা।
(i) 3x + 2y = 5; 2x + 3y = 5
(ii) 4x – 3y = 9 4x – 3y = 8
(a) (i) ৰ যোৰটো সংগত, কিন্তু (ii) ব যোৰটো অসংগত।
(b) (i) আৰু (ii) ৰ যোৰ কেইযোৰ সংগত
(c) (i) আৰু (ii) ৰ যোৰ কেইযোৰ অসংগত
(d) (i) ৰ যোৰটো অসংগত, কিন্তু (ii) ব যোৰটো সংগত।
উত্তৰঃ (a) (i) ব যোৰটো সংগত, কিন্তু (ii) ৰ যোৰটো অসংগত।
প্রশ্নঃ k ৰ কিমানৰ বাবে x + (k + 1) y = 5 আৰু (k + 1) x + 9y = 8k – 1 সমীকৰণৰ অসীম সংখ্যক সমাধান থাকিব?
(a) 1
(b) 0
(c) 2
(d) 3
উত্তৰঃ (c) 2
প্রশ্নঃ যদি m, n ৰ ঘনমূল হয়, তেন্তে । ব মান হ’ব- HSLC ’24
প্রশ্নঃ তলৰ বৈখিক সমীকৰণৰ যোৰকেইটা বিবেচনা কৰা।
(i) 3x + 2y = 5; 2x + 3y = 5
(ii) 2x – 3y = 7 2x – 3y = 8
(a) (i) ৰ যোৰটো অসংগত, কিন্তু (ii) ব যোৰটো সংগত।
(b) (i) আৰু (ii) ৰ যোৰ কেইযোৰ অসংগত
(c) (i) ৰ যোৰটো সংগত, কিন্তু (ii) ৰ যোৰটো অসংগত।
(d) (i) আৰু (ii) ৰ যোৰ কেইযোৰ সংগত
উত্তৰঃ (c) (i) ব যোৰটো সংগত, কিন্তু (ii) ৰ যোৰটো অসংগত।
প্রশ্নঃ p ৰ কি মানৰ বাবে তলত দিয়া সমীকৰণ যোৰৰ এটা অদ্বিতীয় সমাধান আছে? HSLC’25
4x – py + 8 = 0
2x + 2y + 2 = 0
(a) কেরল p = 2 মানৰ বাবে
(b) P42ৰ বাহিৰে সকলো মান
(c) কেবল P = 4 মানৰ বাবে
(d) P4ৰ বাহিৰে সকলো মান
উত্তৰঃ (a) pৰ 4ৰ বাহিৰে সকলো মান
